How Fast are def cdef cpdef?

Code Example

Here is an example of computing the Fibonacci series (badly) that will be done in Python, Cython and C.

First up, Python [Fibo.py]:

def fib(n):
    if n < 2:
        return n
    return fib(n-2) + fib(n-1)

In naive Cython [cyFibo.pyx], it is the same code:

def fib(n):
    if n < 2:
        return n
    return fib(n-2) + fib(n-1)

Optimised Cython where we specify the argument type [cyFibo.pyx]:

def fib_int(int n):
    if n < 2:
        return n
    return fib_int(n-2) + fib_int(n-1)

In Cython calling C generated code. Here we use a def to call a cdef that does the body of the work [cyFibo.pyx]:

def fib_cdef(int n):
    return fib_in_c(n)

cdef int fib_in_c(int n):
    if n < 2:
        return n
    return fib_in_c(n-2) + fib_in_c(n-1)

Now a recursive cpdef:

cpdef fib_cpdef(int n):
    if n < 2:
        return n
    return fib_cpdef(n-2) + fib_cpdef(n-1)

Finally a C extension. We expect this to be the fastest way of computing the result given the algorithm we have chosen:

#include "Python.h"

/* This is the function that actually computes the Fibonacci value. */
static long c_fibonacci(long ord) {
    if (ord < 2) {
        return ord;
    }
    return c_fibonacci(ord - 2) + c_fibonacci(ord -1);
}

/* The Python interface to the C code. */
static PyObject *python_fibonacci(PyObject *module, PyObject *arg) {
    PyObject *ret = NULL;
    assert(arg);
    Py_INCREF(arg);
    if (! PyLong_CheckExact(arg)) {
        PyErr_SetString(PyExc_ValueError, "Argument is not an integer.");
        goto except;
    }
    long ordinal = PyLong_AsLong(arg);
    long result = c_fibonacci(ordinal);
    ret = PyLong_FromLong(result);
    assert(! PyErr_Occurred());
    assert(ret);
    goto finally;
except:
    Py_XDECREF(ret);
    ret = NULL;
finally:
    Py_DECREF(arg);
    return ret;
}

/********* The rest is standard Python Extension code ***********/


static PyMethodDef cFiboExt_methods[] = {
{"fib", python_fibonacci, METH_O, "Fibonacci value."},
{NULL, NULL, 0, NULL}           /* sentinel */
};


#if PY_MAJOR_VERSION >= 3

/********* PYTHON 3 Boilerplate ***********/

PyDoc_STRVAR(module_doc, "Fibonacci in C.");

static struct PyModuleDef cFiboExt = {
PyModuleDef_HEAD_INIT,
"cFibo",
module_doc,
-1,
cFiboExt_methods,
NULL,
NULL,
NULL,
NULL
};

PyMODINIT_FUNC
PyInit_cFibo(void)
{
return PyModule_Create(&cFiboExt);
}

#else

/********* PYTHON 2 Boilerplate ***********/


PyMODINIT_FUNC
initcFibo(void)
{
(void) Py_InitModule("cFibo", cFiboExt_methods);
}

#endif

Benchmarks

First a correctness check on Fibonacci(30):

$ python3 -c "import Fibo, cyFibo, cFibo; print(Fibo.fib(30) == cyFibo.fib(30) == cyFibo.fib_int(30) == cyFibo.fib_cdef(30) == cyFibo.fib_cpdef(30) == cFibo.fib(30))"
True

Now time these algorithms on Fibonacci(30) thus:

$ python3 -m timeit -s "import Fibo" "Fibo.fib(30)"
$ python3 -m timeit -s "import cyFibo" "cyFibo.fib(30)"
$ python3 -m timeit -s "import cyFibo" "cyFibo.fib_int(30)"
$ python3 -m timeit -s "import cyFibo" "cyFibo.fib_cdef(30)"
$ python3 -m timeit -s "import cyFibo" "cyFibo.fib_cpdef(30)"
$ python3 -m timeit -s "import cFibo" "cFibo.fib(30)"

Gives:

Language	Function call	Time (ms)	Speed, Python = 1
Python	Fibo.fib(30)	390	x 1
Cython	cyFibo.fib(30)	215	x 1.8
Cython	cyFibo.fib_int(30)	154	x 2.5
Cython	cyFibo.fib_cdef(30)	5.38	x72
Cython	cyFibo.fib_cpdef(30)	32.5	x12
C	cFibo.fib(30)	5.31	x73

Graphically:

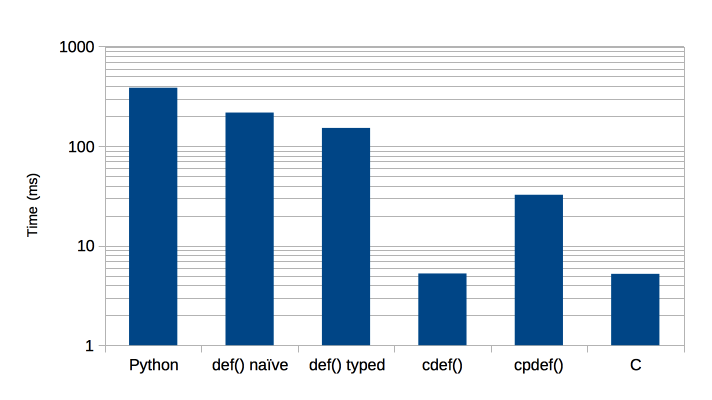
The conclusions that I draw from this are:

• Naive Cython does speed things up, but not by much (x1.8).
• Optimised Cython is fairly effortless (in this case) and worthwhile (x2.5).
• cdef is really valuable (x72).
• cpdef gives a good improvement over def because the recursive case exploits C functions.
• Cython’s cdef is insignificantly different from the more complicated C extension that is our best attempt.

The Importance of the Algorithm

So far we have looked at pushing code into Cython/C to get a performance gain however there is a glaring error in our code. The algorithm we have been using is very inefficient. Here is different algorithm, in pure Python, that will beat all of those above by a huge margin [1]:

def fib_cached(n, cache={}):
    if n < 2:
        return n
    try:
        val = cache[n]
    except KeyError:
        val = fib(n-2) + fib(n-1)
        cache[n] = val
    return val

And timing it for Fibonacci(30) gives:

Language	Function call	Time (ms)	Improvement
Python	Fibo.fib(30)	390	x1
Cython	cyFibo.fib_cdef(30)	5.38	x72
Python	Fibo.fib_cached(30)	0.000231	x1.7e6

Or, graphically:

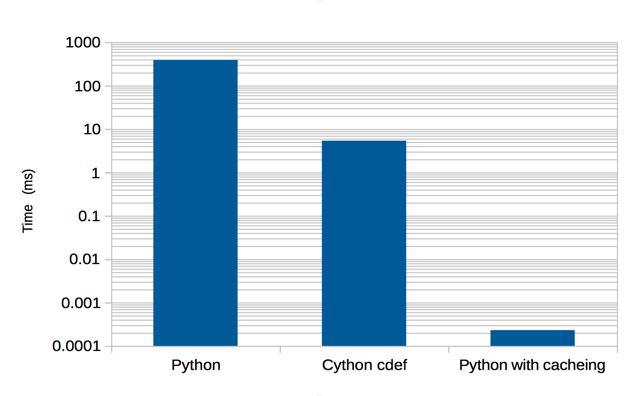
In fact our new algorithm is far, far better than that. Here is the O(N) behaviour where N is the Fibonacci ordinal:

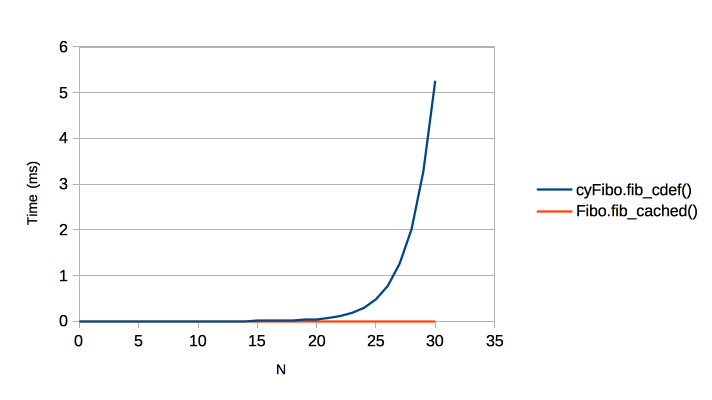
Hammering a bad algorithm with a fast language is worse than using a good algorithm and a slow language.

Footnotes

[1]	If you are using Python3 you can use the functools.lru_cache decorator that gives you more control over cache behaviour.